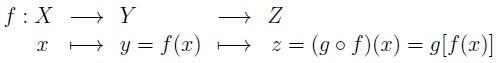Ejemplo
Ejemplo de una composición de funciones
Veamos un ejemplo con las funciones  y
y  .
.

La composición de las funciones  y
y  es:
es:  , pues
, pues
![Rendered by QuickLaTeX.com (g \ o \ f)(x)= g[f(x)]=g(2x)=3(2x)+1=6x+1](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-dac131d24ad19cbacba40016370bd6e0_l3.png)
Al evaluar algunos valores del dominio de la composición  , tenemos que:
, tenemos que:





Problema resuelto
Sean las funciones:


Calcular:
a 
b 
1Sean las funciones:


Calcular:
a 
![Rendered by QuickLaTeX.com g\circ f=g\left [ f(x) \right ]=g\left ( 3x+2 \right )](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-0fe8e9ac588f35dbf2028d9ea5f62854_l3.png)

b 
![Rendered by QuickLaTeX.com f\circ g=f\left [ g(x) \right ]=f\left (\cfrac{x+3}{2x+1} \right )](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-8d8d01b5242f73ec6aaf2a7ea130c119_l3.png)


2Dadas las funciones:



Problema #2
Dadas las funciones:



Calcular:
a 
b 
c 
d 
e 
f Probar que: 
g Probar que: 
2Sean las funciones:



Calcular:
a 
![Rendered by QuickLaTeX.com g\circ f=g\left [ f(x) \right ]=g\left ( \cfrac{1}{2x-1} \right )](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-f4094d49c57d50b26a80e59da4c03827_l3.png)




b 
![Rendered by QuickLaTeX.com f\circ g=f\left [ g(x) \right ]=f\left ( \cfrac{2x-1}{2x+1} \right )](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-46fbe0ac329db8657299b8e123cbf3a2_l3.png)




c 
![Rendered by QuickLaTeX.com h\circ g\circ f=h\left [ \left (g\circ f \right )(x) \right ]](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-5c2fb6fcec2b22669b12f1eb8e9c85a5_l3.png)
Ya sabemos que 
por lo que 

d 
![Rendered by QuickLaTeX.com h\circ f\circ g=h\left [ \left (f\circ g \right )(x) \right ]](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-ae576c032f3f920d1596db0fe9e341eb_l3.png)
Ya sabemos que 
Por lo que 

e 
Para calcular  escribimos la función
escribimos la función  de la forma:
de la forma:

y despejamos la variable 



Cambiamos  por
por  e
e  por
por 

f Probar que: 
![Rendered by QuickLaTeX.com f^{-1}\circ f=f^{-1}\left [ f(x=) \right ]=f^{-1}\left (\frac{1}{2x-1} \right )](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-bb23616ed30ea842bb27a255b6c5069c_l3.png)



g Probar que: 
![Rendered by QuickLaTeX.com f\circ f^{-1}=f\left [ \left ( f^{-1} \right ) \right ]=f\left ( \cfrac{x+1}{2x} \right )](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-1928857a769d3d84d604975b56433d43_l3.png)




La composición de una función con la función inversa es igual a la función identidad

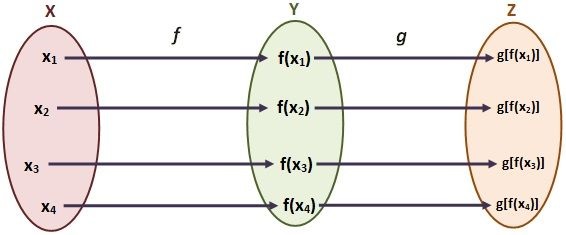
![Rendered by QuickLaTeX.com g[f(x)]](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-cb9326c69c963b52162f20c9b918aabd_l3.png) , a esto se le conoce como composición de funciones
, a esto se le conoce como composición de funciones ![Rendered by QuickLaTeX.com (g \ o \ f)(x)= g[f(x)]](https://www.superprof.es/apuntes/wp-content/ql-cache/quicklatex.com-f65ee6f84d2f4c4925065ce530a1689a_l3.png) (se lee
(se lee  ).
).